DANIELS MATTE 

 

Utsaga

Definition:

 

En utsaga är ett påstående som kan sägas vara sant eller falskt.

 

Exempelvis är ”        är ett irrationellt tal” och ”3 < 2” utsagor medan ”” och ”<” inte är det (man kan inte avgöra om det är sant eller falskt).

 

Sats

Definition:

 

En sats är en utsaga som är en sann. Att utsaga är sann är verifierad (bekräftad) med ett bevis.

 

”       är irrationellt” är en sats och har ett bevis medan ”3 < 2” inte är någon sats, utsagan är ju inte ens sann. 

 

Implikation och ekvavilens

Om vi har två utsagor P och Q. Då kan vi bilda en ny utsaga genom

 

Implikation: P → Q            P medför, implicerar Q                   Om P, så Q

 

Ekvavilens: P ↔ Q              P medför Q och Q medför Q            P om och endast om Q

 

Satstyper

Det finns tre satstyper:

 

1. Enstaka utsaga

 

Exempel:

 

       är ett irrationellt tal

 

2. En implikation P → Q 

 

Exempel:

 

Låt T vara en triangel med sidorna a, b och c där a ≤ b ≤ c. Om T är rätvinklig så gäller:

 

 

 

3. En ekvavilens P ↔ Q

 

Exempel:

 

Ett positivt heltal är delbart med 3 om endast om siffersumman är delbar med 3.

 

Omvändning av sats

Med omvändning av en sats av typ P → Q avses satsen/utsagan Q → P. 

 

 

Bevis av Pythagoras sats och dess omvändning

 

 

Vi ska visa 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Betrakta illustrationen.

 

Vi kan beräkna arean av den stora kvadraten på två sätt:

 

 

1) Som summan av den lilla kvadratens area och trianglarnas area,

 

eller helt enkelt som

 

2.

 

Dessa areor måste ju vara lika. Alltså gäller

 

 

 

Därmed är satsen bevisad. 

 

 

Låt oss nu bevisa omvändningen

 

 

 

 

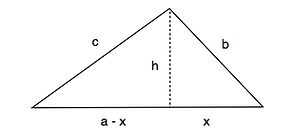
Betrakta illustrationen.

 

 

 

 

 

 

 

 

 

 

 

Vi ska visa att x = 0.

 

Pythagoras sats ger 

 

 

 

 

 

 

 

 

 

 

 

För trubbvinkliga trianglar används samma resonemang, med a + x istället för a - x. 

 

Därmed är satsen bevisad.