DANIELS MATTE 

 

Multiplikationsprincipen

 

Tänk dig att du står och ska beställa din tvårättersmiddag på din favoritrestaurang. Det finns 4 huvudrätter och 3 efterrätter. Medan du väntar på att betala funderar du på: på hur många olika sätt skulle jag kunna kombinera de här rätterna?

 

För varje huvudrätt kan du få 3 efterrätt, antalet kombinationer blir då 4 · 3 = 12.

 

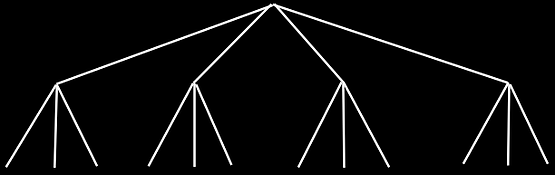
Vi kan rita ett träddiagram:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Om vi kallar vårt första val p och andra val q får vi multiplikationsprincipen:

 

Om båda valen utförs efter varandra kan valen göra på p · q sätt. 

 

Principen gäller även för fler än 2 val.

 

 

 

Permutationer

 

Du har startat en förening med 10 medlemmar och bland dem ska du välja 1, ordförande, 1 sekreterare och en kassör. På hur många sätt kan de väljas?

 

Vi börjar med att välja ordförande. Vi har då 10 valmöjligheter. Då finns det bara 9 möjligheter för sekreteraren (om man inte är både ordförande och sekreterare) kvar. När vi har valt kassör sekreterare har vi bara 8 möjligheter att välja kassören.

 

Enligt multiplikationsprincipen får vi att antalet valmöjligheter är 10 · 9 · 8 = 720.

 

De här valmöjligheterna är ordnade urval och kallas permutationer.

De här valmöjligheterna är ordnade urval och kallas permutationer. Vad menar vi med ordnat urval?

Det är antalet sätt att välja n element bland k med hänsyn till ordningen. Ordningen spelar alltså roll, ba är inte samma sak som ab. Om exempelvis Anna är sekreterare och Bodil ordförande är det inte samma sak som att Bodil är sekreterare och Anna ordförande och räknas som 2 olika val.

 

Vi har valt 3 personer bland 10. Antalet permutationer av 3 personer bland 10 kan då skrivas:

 

P(3, 10) = 10 · 9 · 8

 

Med detta gäller ju bara en specifik situation. Vad blir antalet permutationer av k föremål bland n?

 

 

P(n, k) = n(n - 1)(n - 2)(n - 3) … (n - k + 1)

P(n, k) = antalet k-permutationer av n föremål

 

En speciell permutation har fått ett speciellt skrivsätt. Om vi väljer n föremål bland n får vi:

 

P(n, n) = n(n-1)(n - 2) … 3 · 2 · 1. 

Detta skrivs n! (utläses ”n-fakultet”). Det är alltså produkten av de n första heltalen.

 

4! = 1 · 2 · 3 · 4 

7! =  1 · 2 · 3 · 4 · 5 · 6 · 7.

 

Vårt exempel med P(3, 10) kan också skrivas med hjälp av fakultet:

 

.

 

 

Vi kan skriva om våra formler:

 

P(n, k) =   

 

P(n, n) =    0!  definieras därför som 0!= 1

 

P(n, 0) =  ”0 element kan väljas på ett sätt”

     

 

Kombinationer

 

En grupp på 4 elever har vunnit 2 resor till Paris. Hur många olika sätt kan elevernas resor fördelas?

 

Vi kallar personerna a, b, c och d. Möjligheterna blir då:

 

ab ac ad bc bd cd

ba ca da cb db dc

 

Elevernas resor kan då kombineras på P(4, 2) = 12 sätt. 

 

Men vad är skillnaden mellan, ab och ba? Det är ju fortfarande samma två personer!

 

Man brukar därför prata om kombinationer istället. Då spelar ordningen ingen roll, det är ett oordnat urval. Möjligheterna blir då:

 

ab ac ad bc bd cd

 

Vi skriver att                       (jämför engelskans combination)

 

Ett annat sätt att se kopplingen mellan kombinationer och permutationer är så här:

 

Vi kan bestämma P(4,2) i 2 steg.

 

1. Vi väljer 2 föremål bland 4 där vi inte bryr oss om ordningen. Antalet möjligheter blir då C(4,2).

2. Vi ordnar element2en (föremålen). Det kan göras på 2! sätt.

 

Med multiplikationsprincipen får vi

 

 

Oftast betecknar man C(4,2)   (utläes ”4 över 2”, ”4 välj 3”).

 

Allmänt gäller:

 

Om P(n, k) är antalet permutationer (ordnade urval) och  är antalet kombinationer (oordnade urval) av k element bland n element, så gäller:

 

 

 

Men vad menar vi med ? Hur tolkar vi det?

 

 

Med  menas antalet sätt välja n element bland k utan hänsyn till ordningen.  Det betyder alltså antalet sätt man kan kombinera 3 element bland 6 utan att bry sig om ordningen. 

 

Det är ingen skillnad på att Anna och Bodil åker till Paris och att Bodil och Anna åker till Paris. Det räknas som 1 val.

 

 

 menas antalet sätt att kombinera 3 element bland 3. Det kan man ju bara göra på ett sätt:

 

 

Allmänt gäller att .

 

 

Om vi väljer 2 element bland 5 blir det alltid 3 kvar. Alltså kan vi välja 2 element bland 5 på lika många sätt som 3 element bland 5:

 

      

 

Vi kan visa att det gäller:

 

 

                   

 

 

Allmänt (vi kallar element n och k istället för siffror): 

 

     

 

 

Alltså är  . Det kallas en symmetriegenskap.

 

 

Av detta får vi att  och .

 

Vi får ytterligare en symmetriegenskap, .

 

 

Vi kan tolka  som antalet sätt att välja 0 element bland 5. Det kan man ju bara göra på ett sätt - man väljer inget alls.

 

 

 

Binomialsatsen

 

Hur utvecklar vi ?

 

 

Vi ser att (a+b)4 borde innehålla 4 + 1 = 5 termer, börja med a4 och sluta med a5. Summan av exponenterna verkar bli 4. Vilken tal ska stå framför potenserna, vad är koefficienterna?

 

Koefficienterna står för hur många de olika termerna förekommer. 4 a kan bara kombineras på 1 sätt. Samma sak med 4 b. 

(a + b)(a + b)(a + b)(a + b) 

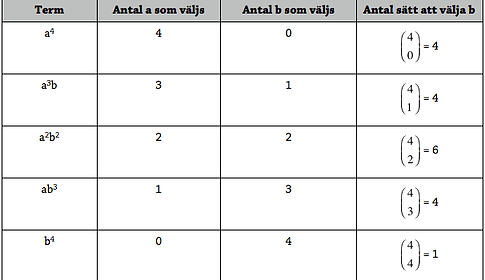
På hur många sätt kan vi kombinera 3 a och 1 b?

 

aaab

aaba

abaa

baaa

Vi ser att antalet kombinationer blir   .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Vi får:

 

 

Eftersom vi har utvecklat binom (polynom med 2 termer) kallas detta binomialsatsen:

 

Av samma anledning kallar vi koefficienterna binomialkoefficienter.

 

Matematikern Blaise Pascal har gett namn åt en tabell som visar de enklaste binomialkoefficienterna. Den kallas Pascals triangel och används för att göra utvecklingar av binom lättare:

 

 

 

n
0	1
1	1 1
2	1  2  1
3	1  3  3  1
4	1  4  6  4  1
5	1  5  10  10  5  1
6	1  6  15  20  15  6  1
7	1  7  21  35  35  21  7  1
8	1  8  28  56  70  56  28  8  1
9	1  9  36  84  126  126  84  36  9  1
10	1  10  45  120  210  252  210  120  45  10  1
11	1  11  55  165  330  462  462  330  165  55  11  1
12	1  12  66  220  495  792  924  792  495  220  66  12  1
13	1  13  78  268 7 15  1287  1716  1716  1287  715  268  78  13 1
14	1  14  91  364  1001  2002  3003  3432  3003  2002  1001  364  91  14  1
15	1  15  105  455  1365  3003  5005  6435  6435  5005  3003 1 365  455  105  15 1

 

 

 

För att leta upp  söker vi i raden n = 6, det femte talet. 

 

Det finns n + 1 platser på en rad eftersom varje rad börjar med . 

 

För talen  och    behöver  vi inte leta i tabellen. 

 

Varje tal (inte 1) är summan av de båda närmaste talen ovanför,  .

 

 

Induktionsbevis

 

Om vi undersöker de n första udda talens summa upptäcker vi följande:

 

1 + 3 = 4

1 + 3 + 5 = 9

1 + 3 + 5 + 7 = 16

1 + 3 + 5 + 7 + 9 = 25

 

De verkar vara kvadrattal!

 

Vi gissar att formeln är:

 

 

Men kan vi bevisa att det gäller, för alla n?

 

Bevis:

 

 

1. n = 1 ger att VL = 1, HL = 12.  Alltså är VL = HL, formeln gäller för n = 1.

 

 

2. Vi bevisar nu att om formeln gäller för n = p gäller den också för n = p + 1.

 

Vi antar att följande gäller:

 

 

 

 

 

Vi påstår att den också gäller för n = p + 1:

 

 

 

 

 

Med hjälp av antagandet bevisar vi att formeln gäller för n = p + 1:

 

 

 

3. Av punkterna 1 och 2 följer att formeln gäller för alla n.

V.S.B

 

 

Den här typen av bevis kallas induktionsbevis. Först visar vi att formeln gäller för n = 1. Sedan gör vi ett antagande att den även gäller för n = p, det kallas ett induktionsantagande. Vi bevisar att om formeln gäller för n = p måste den även gälla för n = p + 1. Av detta följer att formeln gäller för n = 1, 2, 3, … n. 

Det är precis som dominobrickor. Först faller den första brickan. Om en bricka faller, faller nästa också vilket gör att alla brickor faller.